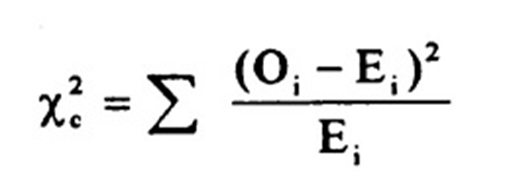A Chi-squared test which can also be written as χ2 test can be any statistical hypothesis test where the sampling distribution of the test statistic is a chi-squared distribution where the null-hypothesis is true.
Chi-squared test also known as Pearson’s chi-squared test.
Chi-squared test is commonly used to determine whether there is great difference between observed frequencies and expected frequencies in one or more categories that we need to judge
This is the formula for Chi-square statistics in chi-square test:
A lower value for Chi-square test means a higher the accuracy of the predicted data.
So if Observed and expected values were equal to each other hence chi-square would be zero.
This event that is unlikely to happen in real life.
What is the Use of Chi-Squared Test?
Chi-squared test is used to test goodness of fit and used to decide whether there is any difference between the observed (experimental) value and the expected (theoretical) value.
The Value of Chi-square test should typically be lower than 0.05 of it to be acceptable as a test for data analysis and later on representation in a more visual basis.
In the following demonstration we will use R programming to perform this test
Initial Environment Setup
But before we get into creating a program let’s just first set up a proper environment for R programming.
To install R programming tool go to the following link and download the software and install it.
For Windows Users:
And Type and Run the following code RGui
install.packages(“ggplot2”)
For Linux Users:
If you are on Linux platform then you can use this fast and easy command used in Linux which can be used to install R. The yum command is used for installing like this:
$ yum install R
For Ubuntu Linux or other Debian-related OSs, a more direct method is:
$ apt-get install r-base
The function that is used to perform Chi-Squared Test is chisq.test ()
It can be expressed as chisq.test (data) where data is the object which contains the dataframe which is in the form of a table containing the count value of the variables in the observation.
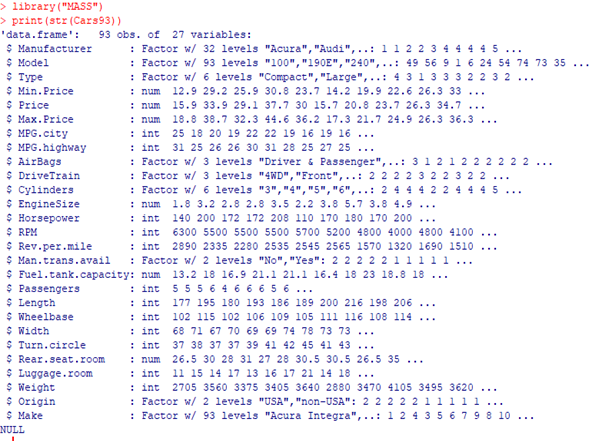
Now in the demo below let us first import the library called as “Mass” which contains data for different models of car in the year 1993.
library(“MASS”)
We can observe the data from the Car93 in Mass Library using the following command
print(str(Cars93))
The Output generated should look something like this.
In the above result we see that the dataset has many Factor variables which can be considered as categorical variables.
In this model let us consider the variables “AirBags” and “Type”.
Through this test we aim to find out any significant correlation between the types of car sold and the type of Air bags it is fitted with.
With this correlation we can observe and estimate which types of cars can sell better with what types of air bags.
# Load the library.
library(“MASS”)
# Create a data frame from the main data set.
car.data <- data.frame(Cars93$AirBags, Cars93$Type)
# Create a table with the needed variables.
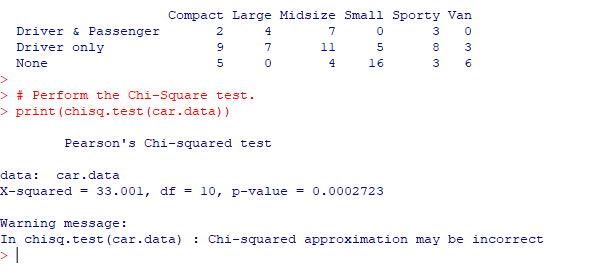
car.data = table(Cars93$AirBags, Cars93$Type)
print(car.data)
# Perform the Chi-Square test.
print(chisq.test(car.data))
On execution of this code in RGui software that is installed in our Computer we should receive the following Output:
If result shows the p-value to have value less than 0.05 then this indicates a significant correlation.
Syllabus of Data Science training in Mumbai